1장 _ 확률이란
- 목차
- 수학의 입장
- 세 개의 문(몬티 홀 문제) - 비행선 시점
- 세 조합(Ω, F, P) - 신의 관점
- 확률변수
- 확률분포
- 실전용 축약법
- Ω는 배후
1.1 수학의 입장
확률이란 무엇인가?
→ “다음 조건을 충족하는 세 조합(Ω, F, P)를 확률 공간이라고 부른다”
1장의 목표는 우리가 어딘지 모르게 가지고 있는 확률의 이미자와 이 추상적인 정의를 연결시키는 것
1.2 세 개의 문(몬티 홀 문제) - 비행선 시점
- 문제 설명
아래 그럼처럼 세 개의 문이 있다. 그 중 하나만 정답이고, 문을 열면 고급차가 있다. 나머지 둘은 오답으로 염소가 있다.
도전자는 세개의 문 중에서 하나만 선택할 수 있다. 사회자는 선택받지 못한 문 중에서 오답을 하나 열어 염소를 보여주면서 선택을 바꿀지 안바꿀지 다시 선택할 수 있는 기회를 준다
이 때, 선택을 바꾸는게 좋을까 아니면 원래의 선택을 고집하는게 좋을까?
▷ 선택지
→ 선택을 바꾼다.
→ 선택을 바꾸지 않는다.
여러분의 선택은?

- 문제 풀이
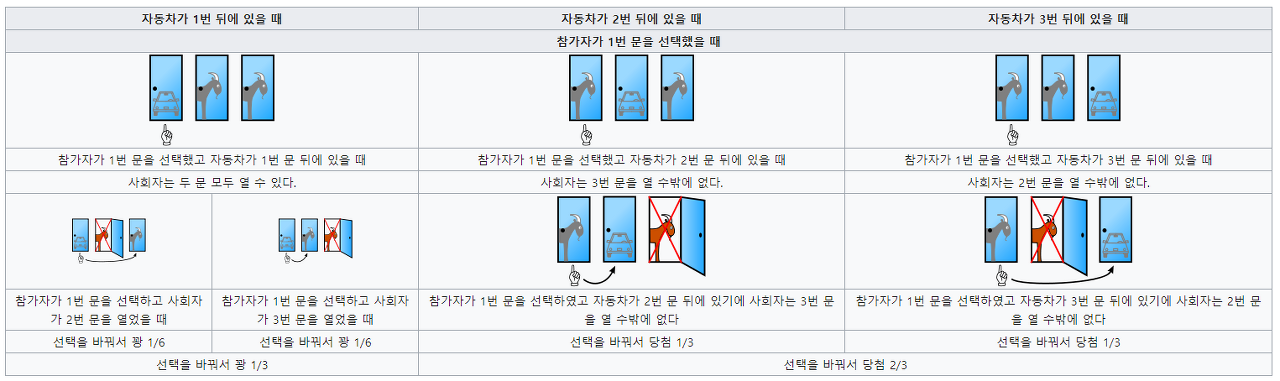
정답으로는 바꾸는것이 더 유리하다.
※ 비행선 시점에서의 번역
위 몬티홀 문제를 큰 광장에 게임장 360개를 설치하고 게임을 병렬로 실시한다고 가정한다.
우리는 비행선에서 타서 위에서 모든 것을 한번에 관찰할 수 있다.
360개의 게임장 중
- 문 ‘가’가 정답 → 120개
- 문 ‘나’가 정답 → 120개
- 문 ‘다’가 정답 → 120개

- 풀이

도전자가 선택을
- 바꾸지 않음 → 120개
- 바꿈 → 240개
이 결과를 보면 다시 선택하는 편이 좋다는 것을 알 수 있다.
1. 3 세 조합(Ω, F, P) - 신의 관점

이전에 비행선에서 내려보는 것처럼 이번에는 신의 관점으로 확률을 바라보기
어느 세계에도 은하가 있고, 지구가 있고, 사람들이 살고 있지만 각 세계에서 일어나는 일은 동일하지 않다. 하지만 각 세계별 동전던지기의 정답(앞,뒤)는 다르겠지만 확률은 같다.
▷ 세 조합(Ω, F, P)은 무엇인가?
평행 세계 전체 집합은 오메가(ω)의 대문자(Ω)로 나타낸다. Ω의 각 원소 ω가 각각 하나의 세계이다.
Ω의 부분집합 A의 면적을 P(A)로 나타낸다. (ex. 동전 던지기 P(앞면) = 0.5) 여기서 P가 세번째를 나타낸다.
남은 두 번째 F는 어렵기 때문에 넘어간다(?)
결국, 평행 세개 전체 집합 Ω와 면적을 측정하는 함수 P가 주어지면 확률 이야기를 할 수 있다.
확률 → 면적 = 선택면적/전체면적 → 확률
1. 4 확률변수
확률변수 = 운에 따라 왔다갔다하는 확정되지 않은 양
확률변수는 X(ω)와 같이 대문자를 사용하는 것이 관례이다.
- 패러럴 월드 전체 집합

- 확률변수 → X


- 확률변수 → Y


- 확률변수 → Z
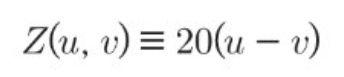

X와 Y의 확률 면적이 같지만 X, Y 자체가 같다는 의미는 아니다.
1. 5 확률 분포
“확률변수”는 각각의 세계까지를 인식하는 개념이지만 “확률분포”는 더 대략적으로 면적만을 신경 쓰는 것
💡 [나무위키] 확률변수(random variable)가 어떤 값을 가질지에 대한 확률을 나타낸다.
확률변수가 취하는 값들의 집합이
- 자연수의 부분 집합과 일대일 대응이 된다 → 이산확률분포
- 실수의 구간을 이룬다 → 연속확률분포
즉, 확률변수의 종류에 따라 크게 이산확률분포와 연속확률분포로 나뉜다.
- X의 확률 분포
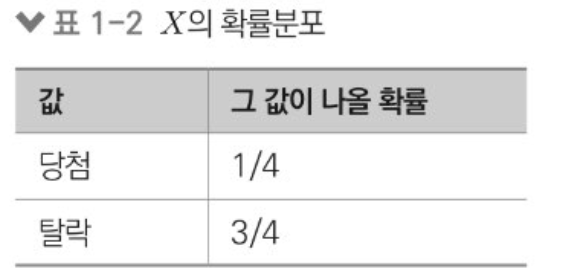
1. 6 실전용 축약법
확률변수는 대문자가 원칙이다. 하지만 문자가 부족해지는 경우 이 원칙이 반드시 지켜지지 않을 때도 있다.
1. 7 Ω는 배후
우리가 관심을 가지는 분야는 면적이지 뒷 본판(Ω)의 모양과 크기가 중요한 것은 아니다.(부피로도 가능)
하지만 전제로 항상 P(Ω) = 1이라는 것은 변하면 안된다.
1. 8 요약
“확률은 면적이다.”
- 확률 변수 : ”확률적인 결과에 따라 결과값이 바뀌는 변수“
- 확률 분포 : 확률 변수가 어떤 값을 가질지에 대한 확률 ( 확률 변수의 분포 상태 )※ 비행선 시점에서의 번역우리는 비행선에서 타서 위에서 모든 것을 한번에 관찰할 수 있다.
'DataScience > 통계-선형대수' 카테고리의 다른 글
| 분산(Variance), 표준편차, 공분산(Covariance), 상관계수, Span, 기저(Basis), Rank (0) | 2021.05.25 |
|---|---|
| 벡터와 매트릭스, 스칼라, Determinant, Cramer's rule (0) | 2021.05.24 |
| 통계학 기초 _ 조건부 확률, 베이즈 정리 (0) | 2021.05.22 |
| 통계학 기초_독립표본 T-검정, Type of Error, 카이제곱검정_One sample 카이검정, Two sample 카이검정, ANOVA분석 (0) | 2021.05.22 |
| 통계학 기초_Effective Sampling, 가설 검정, Student T-test(독립T검정)_One Sample t-test, Two Sample T-test (0) | 2021.05.22 |
![[통계스터디]1주차_확률이란?](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcdUTEP%2FbtrGu3CeBdN%2FAAAAAAAAAAAAAAAAAAAAAI12Nz86GrN4cLzftalaQNCKg9NublFiEbHBREccoUZ0%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Dfm2JVay8umDMOhV3aXyRGy6CASo%253D)