◎ 분산(Variance)
- 분산(variance)은 관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 전체 개수로 나눠서 구한다. 즉, 차이값의 제곱의 평균이다. 관측값에서 평균을 뺀 값인 편차를 모두 더하면 0이 나오므로 제곱해서 더한다.
- 분산은, 데이터가 얼마나 퍼져있는지를 측정하는 방법입니다.
이는 각 값들의 평균으로부터 차이의 제곱 평균입니다.
즉, 분산을 구하기 위해서는 일반적으로 평균을 먼저 계산하여야 합니다.
- 모분산
σ2은 모집단의 분산이다. 관측값에서 모평균을 빼고 그것을 제곱한 값을 모두 더하여 전체 데이터 수 n으로 나눈 것이다.
- 표본분산
s2은 표본의 분산이다. 관측값에서 표본 평균을 빼고 제곱한 값을 모두 더한 것을 n-1로 나눈 것이다.
◎ 표준편차
분산을 구하는 과정에서 우리는 더할때 제곱 값들을 더했습니다.
그렇기 때문에 평균에 비해서 스케일이 커지는 문제가 있는데,
표준 편차는 이를 해결 하기 위해서 제곱 된 스케일을 낮춘 방법입니다.
이는 많은 통계분석 프로세스에서 표준편차를 사용하여 계산하는 이유 중 하나입니다.

▷ python 코드(평균)
v = [243, 278, 184, 249, 207]
def mymean(v):
return sum(v) / len(v)
mymean(v)
<출력>
232.2
▷ python 코드(분산)
v = [243, 278, 184, 249, 207]
def myvar(v):
v1 = []
mean1 = sum(v) / len(v)
for i in v:
v1.append((i-mean1)**2)
return sum(v1) / len(v1)
myvar(v)<출력>
1090.96
▷ python 코드(표준편차)
v = [243, 278, 184, 249, 207]
def mystd(v):
v1 = []
mean1 = sum(v) / len(v)
for i in v:
v1.append((i-mean1)**2)
var1 = sum(v1) / len(v1)
return var1**(1/2)
33.02968361943541<출력>
33.03
▷ python 코드(numpy모듈)
import numpy
arr = [243, 278, 184, 249, 207]
numpy.mean(arr) # 평균
# 232.2
numpy.var(arr) # 분산
# 1090.96
numpy.std(arr) # 표준편차
# 33.02968361943541
numpy.mean(arr), numpy.var(arr), numpy.std(arr)<출력>
(232.2, 1090.96, 33.02968361943541)
◎ 공분산(Covariance)
공분산은 2개의 확률변수의 선형 관계를 나타내는 값이다. 만약 2개의 변수중 하나의 값이 상승하는 경향을 보일 때 다른 값도 상승하는 선형 상관성이 있다면 양수의 공분산을 가진다.
두 확률변수 X와 Y가 어떤 모양으로 퍼져있는지
즉, X가 커지면 Y도 커지거나 혹은 작아지거나 아니면 별 상관 없거나 등을 나타내어 주는 것이다.

Cov(X, Y) > 0 X가 증가 할 때 Y도 증가한다.
Cov(X, Y) < 0 X가 증가 할 때 Y는 감소한다.
Cov(X, Y) = 0 공분산이 0이라면 두 변수간에는 아무런 선형관계가 없으며 두 변수는 서로 독립적인 관계에 있음을 알 수 있다.
◎ 상관계수
상관계수는 두 변수 사이의 통계적 관계를 표현하기 위해 특정한 상관 관계의 정도를 수치적으로 나타낸 계수이다.
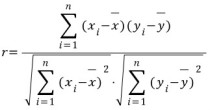
▷ python 코드(공분산, 상관계수)
import numpy as np
var1 = [243, 278, 184, 249, 207]
var2 = [88, 89, 83, 112, 104]
x = np.array(var1)
y = np.array(var2)
mu_x = sum(var1) / len(var1)
mu_y = sum(var2) / len(var2)
res4 = sum((x-mu_x)*(y-mu_y))/len(x) # 공분산
res5 = res4 / (mystd(x)* mystd(y)) # 상관계수
res4, res5<출력>
(57.35999999999999, 0.1586897351257077)
◎ Span
Span 이란, 주어진 두 벡터의 (합이나 차와 같은) 조합으로 만들 수 있는 모든 가능한 벡터의 집합입니다.
◎ Basis
벡터 공간 V의 basis 는, V 라는 공간을 채울 수 있는 선형 관계에 있지 않은 벡터들의 모음입니다. ( span 의 역개념 )
예를 들어, 위의 그림에서 2개의 벡터 (빨강, 파랑)는 벡터 공간 R2 의 basis 입니다.
◎ Rank
- 매트릭스의 rank란, 매트릭스의 열을 이루고 있는 벡터들로 만들 수 있는 (span) 공간의 차원입니다.
- 매트릭스의 차원과는 다를 수도 있으며 그 이유는 행과 열을 이루고 있는 벡터들 가운데 서로 선형 관계가 있을 수도 있기 때문입니다.
☆ 도전
주어진 데이터 (x, y)에 대해서 y = x 라는 벡터에 대해 projection을 계산하는 함수를 작성해보자.
- (x, y) 는 (0, 0) 에서 (x, y)로 가는 벡터라 가정합니다.
이후
- 입력된 데이터를 파란색 선으로,
- y = x 라는 벡터를 빨간색 선으로, 마지막으로
- projection 된 선을 녹색 점선(dashed)으로 그래프에 그리세요.
import matplotlib.pyplot as plt
import numpy as np
plt.xlim(-0,8)
plt.ylim(-0, 8)
v = [7, 4]
b = [17, 17]
plt.gca().set_aspect('equal')
def myProjection(v):
a = v
proj = np.multiply(2.4, b)
plt.arrow(-8, -8, b[0], b[1], linewidth = 3, head_width = .05, head_length = .05, color = 'r')
plt.arrow(0, 0, a[0], a[1], linewidth = 2, head_width = 0.3, head_length = 0.5, color = 'b')
plt.arrow(0, 0, (v[0]+v[1])/2, (v[0]+v[1])/2, linestyle = 'dashed', linewidth = 3, head_width = .05, head_length = .05, color = 'g')
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = 0 * x_vals
plt.plot(x_vals, y_vals, '--', color = 'black')
plt.title("Linearly Independent Vectors")
plt.show()
vprime = myProjection(v)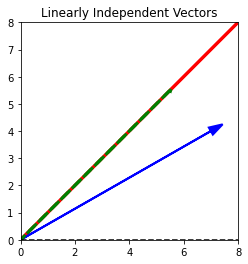
'DataScience > 통계-선형대수' 카테고리의 다른 글
| [통계스터디]1주차_확률이란? (0) | 2022.07.05 |
|---|---|
| 벡터와 매트릭스, 스칼라, Determinant, Cramer's rule (0) | 2021.05.24 |
| 통계학 기초 _ 조건부 확률, 베이즈 정리 (0) | 2021.05.22 |
| 통계학 기초_독립표본 T-검정, Type of Error, 카이제곱검정_One sample 카이검정, Two sample 카이검정, ANOVA분석 (0) | 2021.05.22 |
| 통계학 기초_Effective Sampling, 가설 검정, Student T-test(독립T검정)_One Sample t-test, Two Sample T-test (0) | 2021.05.22 |
