○ 목차
- 활동 함수
- Step Function
- Sigmoid Function
- ReLU
- + hyperbolic tangent (Tanh)
- + Leaky ReLU
- + Softmax
- 과적합을 방지하는 하이퍼 파라미터 튜닝
- Weight Decay
- Weight constriant
- Drop-Out
- Learning rate
활성함수 (Activation function)
신경망 회로에서, 한 노드에 대해 입력값을 다음 노드에 보낼지 말지에 대해 결정하는 함수.
- 계단함수 (Step function)
0을 기준으로 0보다 작으면 데이터를 보내지 않고, 0보다 같거나 크면 데이터를 보내는 유형의 함수이다. 다만 해당 함수는 미분할 수 없으므로, 실제로는 사용되지 않는다.

- Sigmoid Function
위의 Step Function과 비교해서, 훨씬 그래프가 부드러워졌고 연속 가능하다는 것을 알 수 있다. 해당
함수는

으로 구현이 가능하다. Sigmoid 함수의 특징은 다음과 같다.
- 함수값이 (0, 1)로 제한된다.(Binarary값에서 주로 사용)
- 중간값은 1/2다.
- 매우 큰 값을 가지면 함수값은 1이며, 매우 작은 값을 가지면 함수값은 0이다.
그러나 2019년 현재 Sigmoid는 잘 쓰이지 않는다.
이유는, Vanishing Gradient 문제 때문이다. 아래 그래프는, 위 Sigmoid 함수의 미분함수에 대한 그래프이다.

보다시피 x값이 0일때 최고 값은 1/4를 가지며, x값이 매우 클 경우 미분값이 0에 가까워진다. 미분값이 0이라는 것은 기울기가 없다는 것이고, 이러한 상황이 반복적으로 발생시 출력값이 0으로 나타나게 된다. 분명 x가 커지면 값을 다음 노드에 전달할 수 있어야 하는데, 그렇지 않게 되는 것이다.
쉽게 생각해서, 0.99라는 값이 Sigmoid Function을 1회 거쳤을 때 나오는 출력값이라면 이를 10000번 정도 반복하게 되면 2.24877485E-44로, 0에 매우 가까운 값이 나오게 된다. 이는 딥러닝과 같은 학습 시스템에서 결과값에 악영향을 끼치는 요소이다.
- ReLU 함수

ReLU 함수의 특징은 다음과 같다.
- x>0이면 기울기가 1인 직선이고, x<0 이면 함수값이 0이된다.
- sigmoid, tanh 함수와 비교시 학습이 훨씬 빨라진다.
- 연산 비용이 크지않고, 구현이 매우 간단하다.
- x<0 인 값들에 대해서는 기울기가 0이기 때문에 뉴런이 죽을 수 있는 단점이 존재한다.
이 함수의 경우 x값이 커져도 미분함수의 값이 0으로 수렴하지 않기 때문에, 현 시점에서 가장 일반적으로 쓰이는 활성화 함수이다. 이 ReLU 함수를 기반으로 해서 파생된 함수들이 몇 개 더 존재한다. Leaky ReLU의 경우는 ReLU함수에서 발생하는 x<0인 값들에 대해 뉴런이 죽을 수 있는 단점을 보완한 버전이다.
그러나 대체로 ReLU를 먼저 쓰고, 차선책으로 Leaky ReLU와 같은 함수를 쓴다.
Sigmoid, tanh는 쓰지 않는다.
- tanh 함수(Hyperbolic Tangent Function)
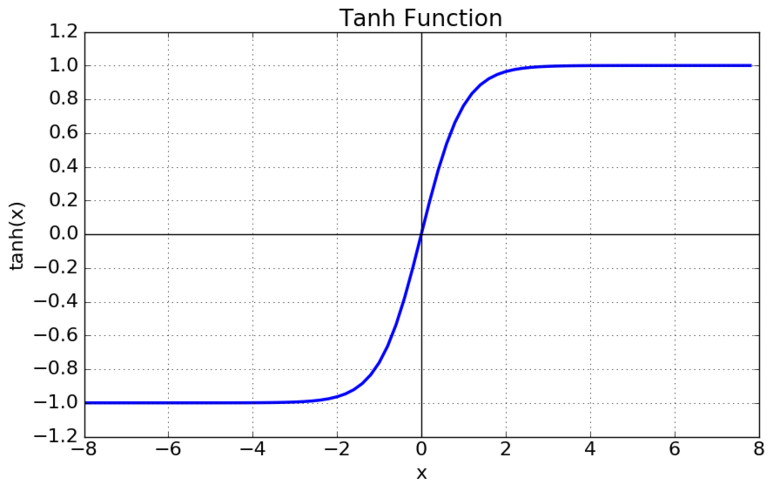
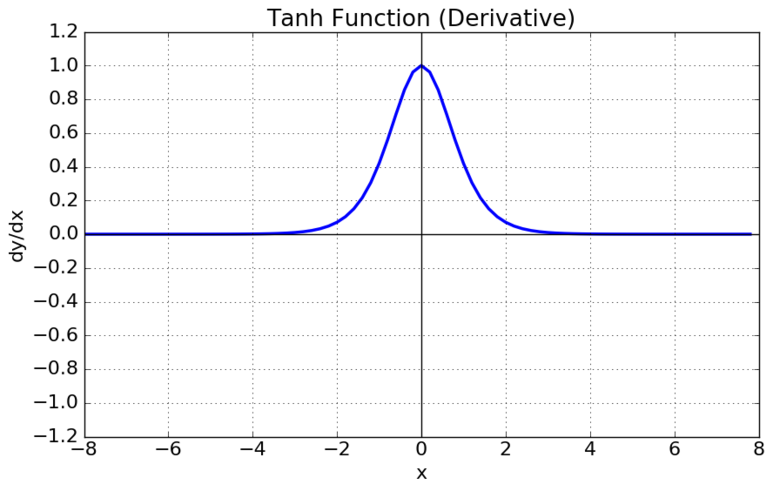
tanh함수는 Sigmoid Function과 유사한 형태를 가지며 Sigmoid Function에 비해 최적화 과정이 느려지는 문제를 해결할 수는 있었으나, 이 함수 역시 미분함수에서 x값이 커질수록 0에 수렴하는 형태로 나타나게 되어 Vanishing Gradient 문제가 발생하게 된다.
- Leaky ReLU

일반적인 ReLU는 음수의 함수는 뉴럼이 활성화되지 않는다. 그렇기 때문에 가중치로 초기화된 뉴런의 경우 결코 발화하지 않고 가중치가 업데이트하지 않는 죽은 뉴런, 쓸데없이 메모리를 차지하는 뉴런으로 될 수 있음을 보여준다.
하지만 Leaky ReLU는 그것을 해결합니다! 파생 기능 왼쪽(음수)에서 0의 경사를 피함으로 해결합니다. 이는 '죽은' 뉴런도 충분한 반복에 의해 재생될 가능성이 있다는 것을 의미한다. 일부 규격에서는 누출되는 좌측의 기울기를 모델의 하이퍼 파라미터로 실험할 수도 있다.
- Softmax Function

sigmoid 함수와 유사하지만 다중 클래스 분류 문제에 더 유용하다. 소프트맥스 함수는 모든 입력 집합을 취하여 최대 1까지 합한 확률로 변환할 수 있다. 이것은 우리가 어떤 출력물 목록을 던질 수 있다는 것을 의미하며, 그것은 확률로 변환할 것이고, 이것은 다중 클래스 분류 문제에 매우 유용하다. 예를 들어 MNIST처럼...
학습 규제 전략 (Regularization Strategies)
Overfitting을 방지하기 위한 기술들에는 여러가지 방법이 있는데 이 블로그에서는 Weight Decay, Dropout, Early Stopping을 설명한다.
- Weight Decay

Weight Decay는 말 그대로 가중치를 감소시키는 기술이다. 아래 그림을 다시한번 보면, 굽이치는 그래프를 나타내려면 큰 가중치가 필요하다. 애초에 큰 가중치를 갖지 못하게 만들면, 다음과 같이 과대적합이 될 수가 없도록 만드는 기술이다.

# Tensorflow에서 데이터를 가져와 규제 하는 코드
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
import keras, os
from tensorflow.keras.datasets import fashion_mnist
# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
print(X_train.shape, X_test.shape)
# 데이터를 정규화 합니다
X_train = X_train / 255.
X_test = X_test /255.
# Weight Decay를 전체적으로 반영한 예시 코드
from tensorflow.keras.constraints import MaxNorm
from tensorflow.keras import regularizers
# 모델 구성을 확인합니다.
model = Sequential([
Flatten(input_shape=(28, 28)),
Dense(64,
kernel_regularizer=regularizers.l2(0.01), # L2 norm regularization
activity_regularizer=regularizers.l1(0.01)), # L1 norm regularization
Dense(10, activation='softmax')
])
# 업데이트 방식을 설정합니다.
model.compile(optimizer='adam'
, loss='sparse_categorical_crossentropy'
, metrics=['accuracy'])
model.summary()
model.fit(X_train, y_train, batch_size=30, epochs=1, verbose=1,
validation_data=(X_test,y_test))- Dropout

Dropout의 경우는 다른 방식으로 overfitting을 방지한다. 모델 자체에 Layer를 추가하는 방식으로 진행이 되는데, 이는 확률적으로 노드 연결을 강제로 끊어주는 역할을 한다. 보톡스를 맞으면 근육을 쓰지 못하게 해서 주름이 생기는 것을 막아버리는데, 뉴럴넷의 보톡스와 같은 존재라고 할 수 있다. 단, 임시로 차단을 하고, 그 연결이 없이 결과를 예측하도록 만들고, 해당 뉴런없이 학습을 진행하기 때문에 과적합을 어느정도 차단할 수 있다.
# seed를 고정합니다.
random.seed(1)
np.random.seed(1)
os.environ["PYTHONHASHSEED"] = str(1)
os.environ['TF_DETERMINISTIC_OPS'] = str(1)
tf.random.set_seed(1)
# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = cifar100.load_data()
# 정규화(전처리)
X_train = X_train / 255.
X_test = X_test / 255.
# 변수 설정을 따로 하는 방법을 적용하기 위한 코드입니다.
batch_size = 100
epochs_max = 20
# model
model = Sequential()
model.add(Flatten(input_shape=(32,32,3)))
model.add(Dense(128*1.1, activation='relu'))
model.add(Dropout(0.1)) # <---------임의로 잡았다.
model.add(Dense(128, activation='relu'))
model.add(Dense(100, activation='softmax'))
# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성함
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
results = model.fit(X_train, y_train, epochs=epochs_max, batch_size=batch_size, verbose=1, validation_data=(X_test,y_test))
test_loss, test_acc = model.evaluate(X_test, y_test, verbose=1) # 0.2100- Early Stopping
조기종료(early stopping)은 Neural Network가 과적합을 회피하도록 만드는 정칙화(regularization) 기법 중 하나이다. 훈련 데이터와는 별도로 검증 데이터(validation data)를 준비하고, 매 epoch 마다 검증 데이터에 대한 오류(validation loss)를 측정하여 모델의 훈련 종료를 제어한다. 구체적으로, 과적합이 발생하기 전 까지 training loss와 validaion loss 둘다 감소하지만, 과적합이 일어나면 training loss는 감소하는 반면에 validation loss는 증가한다. 그래서 early stopping은 validation loss가 증가하는 시점에서 훈련을 멈추도록 조종한다.
Keras에서는 사용자가 early stopping을 손쉽게 적용할 수 있도록 callbacks 이란 기능을 제공한다.
# seed를 고정합니다.
random.seed(1)
np.random.seed(1)
os.environ["PYTHONHASHSEED"] = str(1)
os.environ['TF_DETERMINISTIC_OPS'] = str(1)
tf.random.set_seed(1)
# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = cifar100.load_data()
# 정규화(전처리)
X_train = X_train / 255
X_test = X_test /255
# 학습시킨 데이터를 저장시키기 위한 코드입니다.
checkpoint_filepath = "FMbest.hdf5"
# 변수 설정을 따로 하는 방법을 적용하기 위한 코드입니다.
batch_size = 100
epochs_max = 50
# modeㅣ
model = Sequential()
model.add(Flatten(input_shape=(32, 32, 3)))
model.add(Dense(128, activation='relu'))
model.add(Dense(128, activation='relu'))
model.add(Dense(100, activation='softmax'))
# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성함
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# early stopping
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', min_delta=0, patience=5, verbose=1)
# Validation Set을 기준으로 가장 최적의 모델을 찾기
save_best = keras.callbacks.ModelCheckpoint(filepath=checkpoint_filepath, monitor='val_loss', verbose=1, save_best_only=True,
save_weights_only=True, mode='auto', save_freq='epoch', options=None)
results = model.fit(X_train, y_train, batch_size=batch_size, epochs=epochs_max, verbose=1,
validation_data=(X_test,y_test),
callbacks=[early_stop, save_best])
[참고&출처]
https://blog.naver.com/good5229/221752705030
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=cjh226&logNo=221468928164
'DataScience > 인공지능' 카테고리의 다른 글
| 가상환경 구성 및 주피터(jupyter notebook) 연결 (0) | 2023.01.27 |
|---|---|
| DL.4 _ 신경망 용어정리, Keras Hyperparameters (0) | 2021.08.17 |
| DL.1.1 _ 인공신경망이란, 퍼셉트론 알고리즘 (0) | 2021.08.11 |
| ML _ 교차검증(k-fold, Randomized Search CV, GridSearchCV) (0) | 2021.06.22 |
| ML _ 모델 성능 평가지표 (0) | 2021.06.21 |
