◎ 미분이란
- 미분이란 단어는 작을 미(微)와 나눌 분(分). "작게 나눈다"라는 의미이다.
- 무엇을 작게 나누는 것일까? 바로 함수이다.

미분이라고 하면 어렵다고 생각하는 사람들이 많지만 인공지능에서의 미분은 생각보다 간단하다.
왜? 어차피 계산은 컴퓨터가 하니까ㅎ
미분이 왜 필요한지만 알고 도구(컴퓨터)를 사용하는 법만 익히면 문제 없다.
미분이랑 인공지능을 무슨 관계가 있을까?
인공지능이란 컴퓨터가 사람처럼 주체적으로 결정하고 판단할 수 있는 지능을 부여하는 기술이다.
하지만 컴퓨터는 숫자만 이해하고 숫자로만 말 할 수 있다. 즉, 컴퓨터 자체가 수학이라는 뜻이다.
그럼 인공지능에서 미분이 하는 역할은?
인공지능도 판단할때 실수(오류)라는 것을 한다. 이 때 이 실수(오류)를 0에 수렴하게 하는 방법으로 미분을 사용한다.
AI모델이라는 거대한 함수에 input값이 들어가면 미분을 통해서 오차값이 0에 근사하는 출력값을 뱉어내게 된다.
함수?

함수는 어떤 숫자를 넣으면 다른 숫자가 나오는 상자라고 표현할 수 있는데 인공지능 모델 또한 함수로 구성된 거대한 상자이다.
이런 함수를 활용해서 일단 미분을
특정 파라미터 값 (input)에 대해서 나오는 결과값(output)이 변화하는 정도를 (0에 가까운 부분을 찾기 위해) 계산하는 것
으로 이해하시면 된다.
미분 공식 w/ Python
그럼 미분 공식들에 대해 알아보겠다.
- f(x) = 상수 → f′(x) = 0
f'(x)가 상수 (constant)인 경우에는 x를 아무리 늘리거나 줄여도 늘 같은 숫자이기 때문에 변화가 전혀 없다.
그 말은 즉 변화율이 0이기 때문에 미분계수도 늘 0이다.
- 미분공식으로 만든 2가지 방법의 미분 함수
f(x) = 5
# 예시 1 : 직접 함수를 만드는 방법
def f(x):
return 5
def derivative(fx, x):
delta_x = 1e-5
return (fx(x + delta_x) - fx(x)) / delta_x
print(derivative(f, 1))
# 예시 2 : Scipy의 derivative 활용
from scipy.misc import derivative
# 두 방법의 결과값 비교
derivative(f,1, dx=1e-6) == numerical_derivative(f, 1)- 예시

예시로 위의 식을 미분해보았다.
결과를 직접함수를 만들어서 계산해보겠습니다
def f(x):
return 3*(x**4) + 10
def numerical_derivative(fx, x):
delta_x = 1e-5
return (fx(x + delta_x) - fx(x)) / delta_x
print(numerical_derivative(f, 2))
# 예시 2 : Scipy의 derivative 활용
from scipy.misc import derivative
# 두 방법의 결과값 비교
print(derivative(f,2, dx=1e-5))
derivative(f,2, dx=1e-5) == numerical_derivative(f, 2)<출력>
96.0007200028201
96.0000000031158
- 미분 지식
- e의 x승은 미분해도 e의 x승
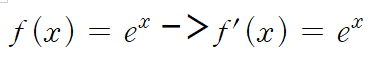
- ln(x)는 미분하면 1/x
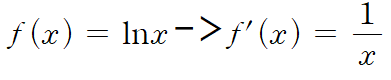
- sin(x)를 미분하면 cos(x)
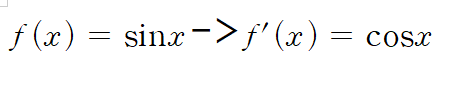
- cos(x)를 미분하면 -sin(x)
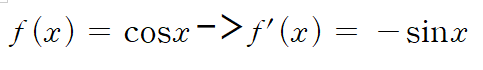
◎ 미분 연습
- x = 5
▷ 예제 1
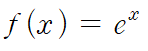
from math import exp
def e_pr(x):
return exp(x)
result = e_pr(5)
result▷ 예제 2
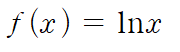
def ln_pr(x):
return 1 / x
result = ln_pr(5)
result▷ 예제 3
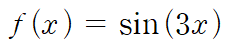
import math
def sin_pr(x):
return 3*math.cos(2*x)
result = sin_pr(5)
result▷ 예제 4
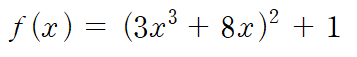
# 방법1 _ 직접 미분한 값을 함수로 지정
def f_pr(x):
return 2*(3*x**3 + 8*x)*(9*x + 8)
result = f_pr(5)
result
# 방법 2 _ scipy 모듈사용해서 미분 구함
from scipy.misc import derivative
def f(x):
return ((3*x**3)+(8*x))**2
result1 = derivative(f,5, dx=1e-6)
result1
'DataScience > 통계-선형대수' 카테고리의 다른 글
| 분산(Variance), 표준편차, 공분산(Covariance), 상관계수, Span, 기저(Basis), Rank (0) | 2021.05.25 |
|---|---|
| 벡터와 매트릭스, 스칼라, Determinant, Cramer's rule (0) | 2021.05.24 |
| 통계학 기초 _ 조건부 확률, 베이즈 정리 (0) | 2021.05.22 |
| 통계학 기초_독립표본 T-검정, Type of Error, 카이제곱검정_One sample 카이검정, Two sample 카이검정, ANOVA분석 (0) | 2021.05.22 |
| 통계학 기초_Effective Sampling, 가설 검정, Student T-test(독립T검정)_One Sample t-test, Two Sample T-test (0) | 2021.05.22 |
