728x90
정렬 알고리즘이란?
- 데이터를 특정한 기준에 따라 순서대로 나열
- 컴퓨터 분야에서 중요시되는 문제 중 하나
- 탐색에 용이
- 프로그래밍과 알고리즘 이해에 많은 도움이
정렬 알고리즘 종류
1. 선택 정렬
- 가장 기초적인 알고리즘
- 전체 범위에서 차례대로 가장 작은 숫자를 탐색하고 가장 왼쪽부터 차례대로 교환하는 방식
- 전체 범위를 돌며 작은 숫자를 선택하여 정렬하는 것이므로 선택정렬이라고 함.

- 가장 왼쪽부터 작은수대로 정렬
코드
for i in range(len(array)):
min_index = i
for j in range(i+1, len(array)):
if array[min_index] > array[j]:
min_index= j
#스와프 코드
array[i], array[min_index] = array[min_index], array[i]
print(array)#스와프 코드
array= [3,5]
array[0], array[1] = array[1], array[0]
print(array)
[5,3]- 장점 : 자료 이동 횟수가 미리 결정
- 단점 : 값이 같은 요소가 있다면 상대적인 위치가 변경될 수 있다.
- 시간복잡도(최악, 최선, 평균) : O(n^2)
2. 삽입 정렬
- 가장 기초적인 알고리즘
- 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열부분과 비교하여 자신의 위치를 찾아 삽입하는 방식
- 이미 정렬된 배열에서 자기 자신의 위치를 찾아 삽입된다고 하여 삽입정렬이라고 함


코드
for i in range(1, len(array)):
for j in range(i, 0, -1):
if array[j] < array[j-1]:
array[j], array[j-1] = array[j-1], array[j]
else:
break- 장점 : 최선의 경우 O(n)
- 단점 : 요소가 너무 많으면 비교적 많은 이동을 해야하므로 성능이 좋지 않다
- 시간복잡도
- 최악 : O(n^2)
- 평균 : O(n^2)
- 최선 : O(n)
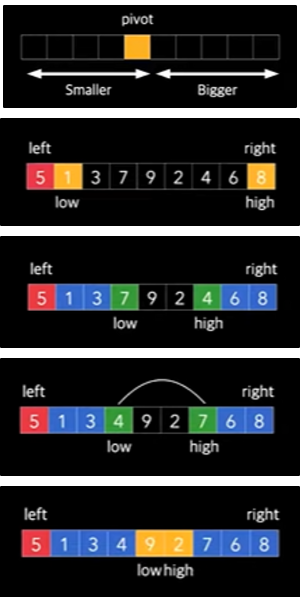
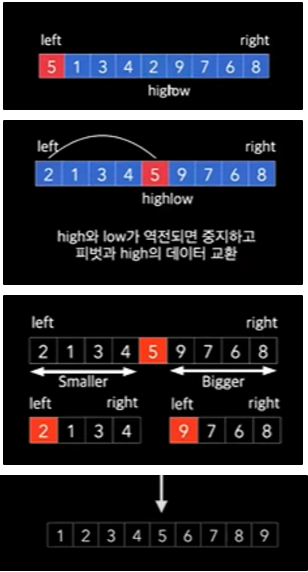
3. 퀵정렬
- 복잡하지만 효율적인 알고리즘
- 특정요소를 기준점으로 잡고 기준점보다 작은 요소는 왼쪽, 큰요소는 오른쪽, 왼쪽과 오른쪽을 각각 정복하는 방식
- 다른 정렬 알고리즘보다 효율적이고 빨라 퀵 정렬이라고 한다.
코드
def quick_sort(array, start, end):
if start >= end: #원소가 1개인 경우 종류
return
pivot = start
left = start +1
right = end
while left <= right:
while left <= end and array[left] <= array[pivot]:
left +=1
while right > start and array[right] >= array[pivot]:
right -= 1
if left> right:
array[left], array[pivot] = array[pivot], array[right]
else:
array[left], array[right] = array[right], array[left]
quick_sort(array, start, right-1)
quick_sort(array, right+1, end)def quick_sort(array):
if len(array) <= 1:
return array
pivot = array[0]
tail = array[1:]
left_side = [x for x in tail if x <= pivot]
right_side = [x for x in tail if x> pivot]
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
- 장점 : 평균 실행시간이 다른 알고리즘보다 빠르다
- 단점 : Pivot에 따라서 성능차이가 심하다
- 시간복잡도 : pivot이 중간에 가까운 값을 찾을 수록 성능이 좋다.
- 최악 : O(n^2)
- 평균 : O(nlogn)
- 최선 : O(nlogn)
4. 계수정렬
- 특정한 조건이 부합할 때만 사용할 수 있지만 매우 빠른 정렬 알고리즘
- 데이터의 크기범위가 제한되어 정수 형태로 표현할 수 있을 때만 사용가능
- 별도의 리스트 선언, 정렬에 대한 정보 담기
코드
count = [0] * (max(array) + 1)
for i in range(len(array)):
count[array[i]] += 1
for i in range(len(count)):
for j in range(count[i]):
print(i, end=' ')
- 시간 복잡도
- O(N+K)
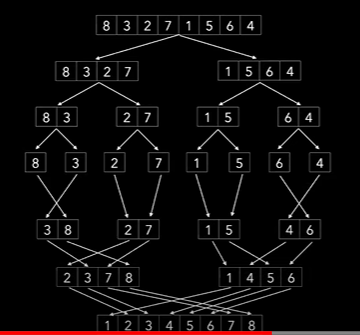
5. 병합정렬(참고)
- 복잡하지만 효율적인 알고리즘
- ‘분할 정복’이라는 알고리즘 디자인 기법에 근거하여 복잡한 문제를 복잡하지 않은 문제로 분할하여 정복하는 방식
- 병합 정렬은 분할보다 병합과정에서 정렬이 이루어짐
def merge_sort(arr):
if len(arr) < 2:
return arr
mid = len(arr) // 2
low_arr = merge_sort(arr[:mid])
high_arr = merge_sort(arr[mid:])
merged_arr = []
l = h = 0
while l < len(low_arr) and h < len(high_arr):
if low_arr[l] < high_arr[h]:
merged_arr.append(low_arr[l])
l += 1
else:
merged_arr.append(high_arr[h])
h += 1
merged_arr += low_arr[l:]
merged_arr += high_arr[h:]
return merged_arr- 장점 : 데이터 분포의 영향을 덜 받는다
- 단점 : 요소를 배열로 구성하면 임시 배열이 필요하다
- 시간 복잡도 (최선, 평균 최악) : O(nlogn)
정렬 알고리즘 선택시 고려사항
- 시간 복잡도가 전부는 아니다
- 알고리즘별로 각각 장단점이 있으므로 상황에 맞게 선택
1. 안정성
O - 버블, 삽입, 병합
X - 선택, 퀵(안정판이 존재하긴 함), 힙
2. 공간복잡도
1 - 버블, 삽입, 선택, 힙
n - 병합
logn - 퀵
3. 지역성
4. 키값들의 분포 상태
5. 데이터의 양
6.초기 데이터의 배열상태
7. 사용 컴퓨터 특성
파이썬의 정렬 라이브러리
- sorted() : 병합 정렬 기반
result = sorted(array)- sort() : 리스트 변수에서 사용
array.sort()- key를 매개변수로 받을 수 있음
def setting(data):
return data[1]
ressult = sorted(array, key = setting)
print(result)정렬 라이브러리의 시간복잡도
최악 : O(NlogN)
- 정렬 라이브러리로 풀 수 있는 문제 : 단순히 정렬기법을 알고 있는지 물어보는 문제
- 정렬 알고리즘의 원리에 대해 물어보는 문제 : 선택, 삽입, 퀵정렬 등의 원리를 알고 있어야 함
- 더 빠른 정렬이 필요한 문제 : 계수 정렬등의 다른 알고리즘 이용
예제 문제
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
2437번: 저울
하나의 양팔 저울을 이용하여 물건의 무게를 측정하려고 한다. 이 저울의 양 팔의 끝에는 물건이나 추를 올려놓는 접시가 달려 있고, 양팔의 길이는 같다. 또한, 저울의 한쪽에는 저울추들만 놓
www.acmicpc.net
#계수정렬
https://www.acmicpc.net/problem/10989
10989번: 수 정렬하기 3
첫째 줄에 수의 개수 N(1 ≤ N ≤ 10,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 10,000보다 작거나 같은 자연수이다.
www.acmicpc.net
728x90
'코딩테스트' 카테고리의 다른 글
| 정렬_심화25) 실패율 _ python (0) | 2023.09.25 |
|---|---|
| 정렬_심화24) 안테나 _ python (0) | 2023.09.25 |
| BFS&DFS_심화21) 인구이동 _ python (0) | 2023.09.25 |
| BFS&DFS_심화20) 감시 피하기 _ python (0) | 2023.09.25 |
| BFS&DFS_심화19) 연산자 끼워 넣기 _ python (0) | 2023.09.25 |
